Hình tam giác là gì ? Các công thức tính toán chu vi, diện tích tam giác

Hình tam giác là một trong những khái niệm quan trọng trong toán học và hình học. Nó không chỉ có ứng dụng trong lĩnh vực học tập mà còn trong đời sống hàng ngày. Trong bài viết này, chúng ta sẽ tìm hiểu về tam giác và các công thức tính toán liên quan đến nó.

Hình tam giác là gì?

Hình tam giác là một hình học có ba cạnh và ba góc. Tam giác có ba đỉnh và ba cạnh, trong đó mỗi cạnh là một đoạn thẳng nối hai đỉnh. Góc của tam giác là góc được tạo bởi hai cạnh gặp nhau tại một đỉnh.

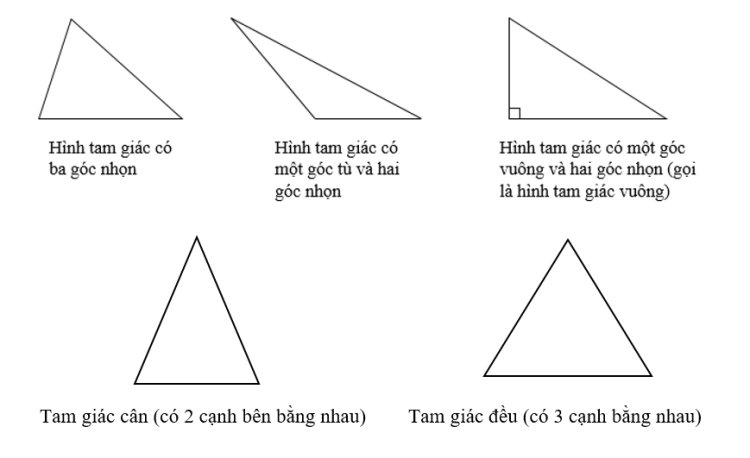
Tam giác có một số thuộc tính cơ bản:

1. Cạnh: Tam giác có ba cạnh. Cạnh có thể có độ dài khác nhau hoặc bằng nhau.

2. Đỉnh: Tam giác có ba đỉnh. Đỉnh được ký hiệu bằng các chữ cái hoa A, B và C.

3. Góc: Tam giác có ba góc. Góc được ký hiệu bằng các chữ cái thường a, b và c, tương ứng với các đỉnh A, B và C.

4. Chu vi: Chu vi của tam giác là tổng độ dài của tất cả các cạnh của tam giác.

5. Diện tích: Diện tích của tam giác có thể được tính bằng nửa tích chất của một cạnh và độ dài đoạn vuông góc từ đỉnh đó đến đường thẳng chứa cạnh còn lại.

Tam giác có nhiều loại khác nhau dựa trên các đặc điểm của nó, bao gồm tam giác đều (các cạnh và góc đều nhau), tam giác vuông (có một góc vuông), tam giác cân (có hai cạnh bằng nhau), tam giác đều cân (có cả cạnh và góc đều nhau) và nhiều loại khác nữa.

Hình tam giác là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong các lĩnh vực khác nhau như hình học, vật lý, kỹ thuật và thiết kế.

Xem thêm: Công thức tính chu vi, diện tích hình tam giác và mối liên hệ giữa chu vi và diện tích trong tam giác

Tìm hiểu về tam giác và các công thức tính toán

Tam giác là một hình học có ba cạnh và ba góc. Có nhiều loại tam giác khác nhau, bao gồm tam giác đều, tam giác vuông, tam giác cân và tam giác nhọn. Mỗi loại tam giác đều có các tính chất riêng và các công thức tính toán khác nhau. Hãy cùng tìm hiểu về một số khái niệm cơ bản và công thức tính toán liên quan đến tam giác.

1. Tam giác đều

Tam giác đều là tam giác có cả ba cạnh bằng nhau và cả ba góc đều bằng nhau. Đây là một loại tam giác đặc biệt và có nhiều tính chất thú vị. Dưới đây là một số công thức tính toán cho tam giác đều:

• Chu vi tam giác đều: Để tính chu vi tam giác đều, ta có công thức: chu vi = 3 x độ dài cạnh.
• Diện tích tam giác đều: Để tính diện tích tam giác đều, ta có công thức: diện tích = căn bậc hai(3) / 4 x (độ dài cạnh)^2.

2. Tam giác vuông

Tam giác vuông là tam giác có một góc vuông, tức là một góc đo 90 độ. Đây cũng là một loại tam giác phổ biến và có nhiều công thức tính toán quan trọng. Dưới đây là một số công thức tính toán cho tam giác vuông:

• Định lý Pythagoras: Định lý Pythagoras là một định lý quan trọng trong tam giác vuông. Nó nói rằng trong một tam giác vuông, bình phương của độ dài cạnh huyền bằng tổng bình phương của độ dài hai cạnh góc vuông. Công thức của định lý Pythagoras là: a^2 + b^2 = c^2, trong đó a và b là độ dài hai cạnh góc vuông và c là độ dài cạnh huyền.
• Tỉ lệ giữa các cạnh trong tam giác vuông: Trong tam giác vuông, có một tỉ lệ đặc biệt giữa các cạnh gọi là tỉ lệ tam giác vuông. Tỉ lệ này được ký hiệu bằng a:b:c, trong đó a, b và c lần lượt là độ dài các cạnh góc vuông, và tỉ lệ này thường được viết dưới dạng số nguyên nhỏ nhất.

3. Tam giác cân

Tam giác cân là tam giác có ít nhất hai cạnh bằng nhau. Đây là một loại tam giác đặc biệt và cũng có các công thức tính toán riêng. Dưới đây là một số công thức tính toán cho tam giác cân:

• Độ dài đường cao: Đường cao của tam giác cân được định nghĩa là đường thẳng kết nối đỉnh vuông góc với đáy tương ứng. Độ dài đường cao có thể được tính bằng công thức: đường cao = căn bậc hai(2 x diện tích) / độ dài đáy.
• Công thức Heron: Công thức Heron được sử dụng để tính diện tích tam giác cân khi chỉ biết độ dài các cạnh. Công thức này được viết như sau: diện tích = căn bậc hai(p x (p - a) x (p - b) x (p - c)), trong đó p là nửa chu vi của tam giác (p = (a + b + c) / 2).

4. Tam giác nhọn

Tam giác nhọn là tam giác có tất cả ba góc nhọn, tức là các góc đo đều nhỏ hơn 90 độ. Trên thực tế, hầu hết các tam giác mà chúng ta gặp phải trong đời sống hàng ngày đều là tam giác nhọn. Đây là loại tam giác phổ biến và có nhiều tính chất thú vị. Một số công thức tính toán cho tam giác nhọn bao gồm:

• Công thức Sine: Công thức Sine là một trong những công thức quan trọng trong tam giác nhọn. Nó cho phép chúng ta tính toán độ lớn của các góc trong tam giác. Công thức này được viết như sau: sin(A) = a / c, sin(B) = b / c, sin(C) = a / b, trong đó A, B và C lần lượt là các góc tam giác, và a, b, c là độ dài các cạnh tương quan
• Định lý Cosine: Định lý Cosine là một công thức khác để tính toán độ lớn của các góc trong tam giác. Công thức này liên quan đến tỉ lệ giữa độ dài các cạnh và cosin của các góc. Công thức này được viết như sau:

1. cos(A) = (b^2 + c^2 - a^2) / (2bc)
2. cos(B) = (a^2 + c^2 - b^2) / (2ac)
3. cos(C) = (a^2 + b^2 - c^2) / (2ab)

5. Công thức tính toán khác

Ngoài những công thức tính toán cơ bản cho các loại tam giác đã đề cập ở trên, còn có một số công thức khác liên quan đến tam giác. Dưới đây là một số công thức quan trọng khác:

• Công thức tính toán chu vi: Chu vi của một tam giác có thể được tính bằng tổng độ dài các cạnh. Công thức này đơn giản là: chu vi = a + b + c.
• Công thức tính toán diện tích: Diện tích của một tam giác có thể được tính bằng nhiều cách khác nhau, như sử dụng công thức Heron, sử dụng đường cao, sử dụng định lý Sine và Cosine, hoặc sử dụng các công thức khác tùy thuộc vào thông tin đã biết về tam giác.
• Công thức tính toán các góc trong tam giác: Ngoài công thức Sine và Cosine đã đề cập ở trên, còn có các công thức khác để tính toán độ lớn của các góc trong tam giác, như công thức Tangent (tan), công thức Cosecant (csc), công thức Secant (sec) và công thức Cotangent (cot).

Câu hỏi thường gặp

1. Tam giác vuông có những tính chất gì đặc biệt?

Tam giác vuông có một góc vuông, tức là một góc đo 90 độ. Tính chất đặc biệt của tam giác vuông là:

• Định lý Pythagoras áp dụng cho tam giác vuông.
• Tỉ lệ tam giác vuông giữa các cạnh.
• Tính chất của các góc trong tam giác vuông, như góc bằng 30 độ, 45 độ và 60 độ.

2. Làm thế nào để tính diện tích của một tam giác?

Có nhiều cách để tính diện tích của một tam giác, bao gồm sử dùng công thức Heron, sử dụng đường cao, sử dụng công thức Sine và Cosine, và sử dụng các công thức khác tùy thuộc vào thông tin đã biết về tam giác. Hãy xem xét ví dụ sau để minh họa:

Giả sử chúng ta có một tam giác ABC với độ dài các cạnh a, b và c. Để tính diện tích của tam giác này, chúng ta có thể sử dụng công thức Heron:

• Nửa chu vi của tam giác: p = (a + b + c) / 2.
• Diện tích của tam giác: diện tích = căn bậc hai(p x (p - a) x (p - b) x (p - c)).

Áp dụng công thức này, chúng ta có thể tính toán diện tích của tam giác ABC dựa trên thông tin về độ dài các cạnh a, b và c.

3. Tam giác có thể có bao nhiêu loại?

Tam giác có nhiều loại khác nhau, bao gồm:

• Tam giác đều: Có cả ba cạnh và ba góc đều bằng nhau.
• Tam giác vuông: Có một góc vuông, tức là một góc đo 90 độ.
• Tam giác cân: Có ít nhất hai cạnh bằng nhau.
• Tam giác nhọn: Có tất cả ba góc nhọn, tức là các góc đo đều nhỏ hơn 90 độ.
• Tam giác tù: Có một góc tù, tức là một góc đo lớn hơn 90 độ.
• Tam giác vuông cân: Có cả một góc vuông và hai cạnh bằng nhau.

Mỗi loại tam giác có các tính chất và công thức tính toán riêng biệt.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về tam giác và các công thức tính toán liên quan đến nó. Tam giác là một hình học quan trọng và có nhiều ứng dụng trong đời sống hàng ngày và các lĩnh vực khác nhau. Chúng ta đã tìm hiểu về các loại tam giác như tam giác đều, tam giác vuông, tam giác cân và tam giác nhọn, cũng như các công thức tính toán cho mỗi loại tam giác. Bằng cách áp dụng các công thức này, chúng ta có thể tính toán chu vi, diện tích và các thông số khác của tam giác.