Trực tâm là gì? Tính chất và cách xác định trực tâm trong tam giác

Tìm hiểu chi tiết về trực tâm trong toán học là một hành trình khám phá về một khái niệm quan trọng và độc đáo trong hình học. Trực tâm không chỉ là một điểm đơn thuần trong tam giác mà còn là trung tâm của nhiều tính chất và mối quan hệ phức tạp trong hình học. Qua việc nghiên cứu và hiểu rõ về trực tâm, chúng ta có cơ hội khám phá sâu hơn về cấu trúc và các đặc điểm đặc biệt của tam giác.

Trong bài viết này, chúng ta sẽ khám phá từng khía cạnh của trực tâm, từ định nghĩa cơ bản đến các tính chất và mối quan hệ với các phần khác của tam giác. Chúng ta cũng sẽ tìm hiểu về cách xác định trực tâm trong tam giác và những ứng dụng thực tế của khái niệm này trong toán học và các lĩnh vực khác. Hãy cùng nhau bắt đầu hành trình khám phá về trực tâm và khám phá sự kỳ diệu của nó trong lĩnh vực toán học!

Trực tâm là gì?

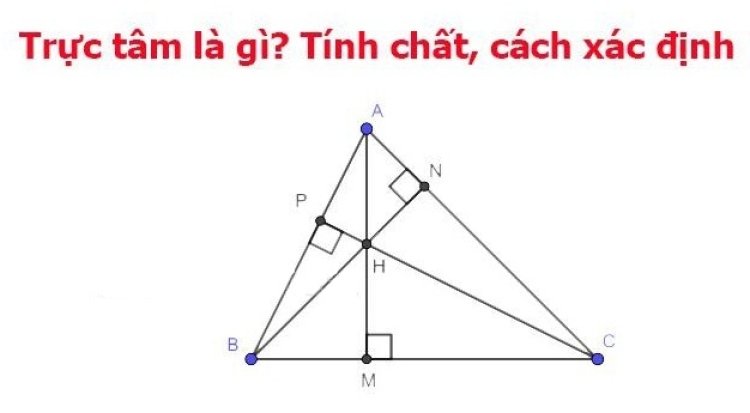
Trực tâm của tam giác là giao điểm của 3 đường cao, nghĩa là giao điểm của các đường thẳng từ mỗi đỉnh của tam giác đến cạnh đối diện của nó tạo thành một góc vuông. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.

Như vậy, 3 đường cao xuất phát từ 3 đỉnh tới cạnh đối diện của một tam giác sẽ giao nhau tại 1 điểm gọi là trực tâm. Trực tâm của tam giác có thể nằm bên trong hoặc bên ngoài của tam giác đó tùy thuộc vào mỗi loại hình tam giác khác nhau, cụ thể là:

• Nếu tam giác có 3 góc nhọn (nhỏ hơn 90 độ) thì trực tâm sẽ nằm trong tam giác.
• Nếu tam giác có 1 góc tù (lớn hơn 90 độ) thì trực tâm sẽ nằm bên ngoài tam giác.

Trong một số hình tam giác đặc biệt thì trực tâm có thể là:

• Trực tâm của tam giác vuông chính là đỉnh góc vuông của tam giác.
• Trực tâm của tam giác đều cũng chính là trọng tâm, tâm của đường tròn nội ngoại tiếp của tam giác đó. Hay nói cách khác, trực tâm của tam giác đều cách đều 3 đỉnh và 3 cạnh của tam giác đó.

Ví dụ: Trong tam giác ABC kẻ 3 đường cao là AI, BK, CE giao nhau tại điểm H. H được gọi là trực tâm của tam giác ABC. Hình minh họa bên dưới.

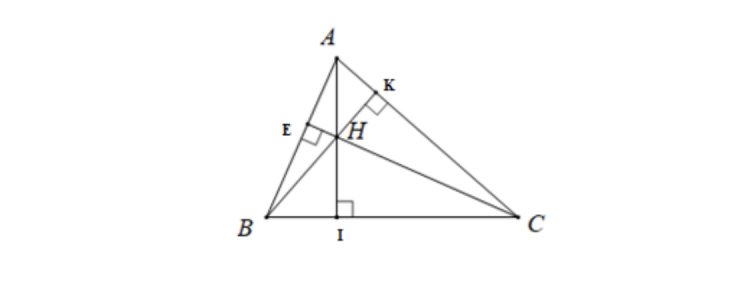
Tính chất của trực tâm trong tam giác

Trực tâm của tam giác có một số tính chất dưới đây

• Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đến trung điểm của một cạnh: Khoảng cách này bằng 1/2 khoảng cách từ trực tâm tới đỉnh còn lại của tam giác. Điều này có nghĩa là nếu chúng ta vẽ đường tròn ngoại tiếp tam giác và nối trực tâm với trung điểm của một cạnh, thì khoảng cách từ trung điểm đó tới tâm đường tròn ngoại tiếp tam giác sẽ bằng 1/2 khoảng cách từ trực tâm tới đỉnh còn lại của tam giác.

• Đường trung trực trong tam giác cân: Trong tam giác cân, đường trung trực tương ứng với cạnh đáy cũng là đường cao, đường phân giác và đường trung tuyến của tam giác đó. Điều này có nghĩa là trong tam giác cân, đường trung trực nối trực tâm của tam giác với trung điểm của cạnh đáy là một trong ba đường cao, đường phân giác và đường trung tuyến của tam giác.

• Tam giác cân: Tam giác được gọi là tam giác cân khi đường trung tuyến đồng thời là đường phân giác hoặc đường cao hoặc đường trung trực. Đây là một định lý quan trọng về tính chất của tam giác cân.

• Vị trí của trực tâm trong tam giác nhọn: Trực tâm của tam giác nhọn trùng với tâm đường tròn nội tiếp tam giác, được tạo bởi 3 đỉnh và 3 chân đường cao tương ứng.

• Điểm đối xứng với trực tâm qua cạnh đáy của tam giác: Điểm đó nằm trên đường tròn ngoại tiếp tam giác, được gọi là điểm đối xứng với trực tâm qua cạnh đáy. Đây là một điểm quan trọng liên quan đến định lý Carnot trong hình học tam giác.

Việc nắm vững các tính chất của trực tâm sẽ giúp bạn dễ dàng giải được các bài toán trong hình học. Vì vậy, bạn hãy cố gắng ghi nhớ các tính chất bên trên nhé để thuận lợi hơn trong quá trình giải các bài toán về hình học có liên quan đến trực tâm của tam giác.

Cách xác định trực tâm của tam giác

Cách để xác định trực tâm của tam giác thì bạn vẽ 3 đường cao của tam giác đó. Tuy nhiên, trên thực tế, chúng ta chỉ cần vẽ 2 trong 3 đường cao, giao điểm của chúng ở đâu chính là trực tâm của tam giác đó.

Bạn cũng nên nhớ một số điểm sau để kiểm tra xem mình đã xác định đúng trực tâm của tam giác hay không:

• Trực tâm của tam giác vuông chính là đỉnh của góc vuông.
• Trực tâm của tam giác có 3 góc nhọn nằm bên trong tam giác.
• Trực tâm của tam giác có 1 góc tù nằm bên ngoài tam giác.

Ngoài ra, còn có nhiều cách để xác định trực tâm của tam giác tùy theo từng bài toán cụ thể.

Trực tâm của tam giác nhọn

Kẻ hai đường cao từ hai đỉnh của tam giác về hai cạnh đối diện (đoạn thẳng vuông góc từ đỉnh B và C tới cạnh tương ứng). Hai đường cao này sẽ cắt nhau tại một điểm duy nhất, đó chính là trực tâm của tam giác.

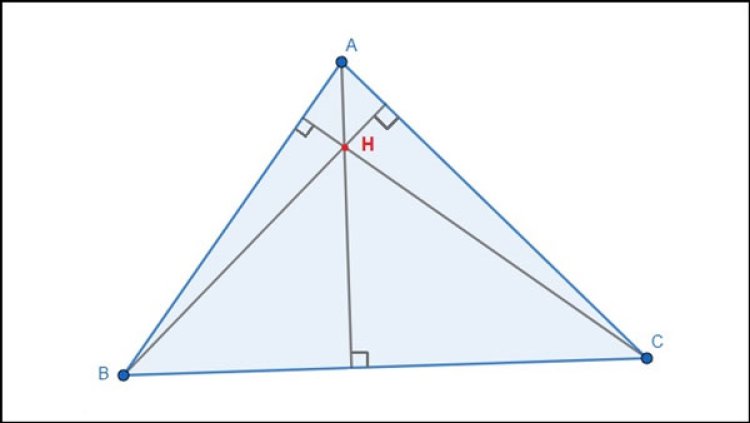
Tam giác nhọn ABC có trực tâm H nằm ở miền trong tam giác và có vị trí gần trung điểm của các cạnh.

Trực tâm của tam giác vuông

Trực tâm chính là đỉnh góc vuông.

Ví dụ: Tam giác vuông EFG có trực tâm H trùng với góc vuông E.

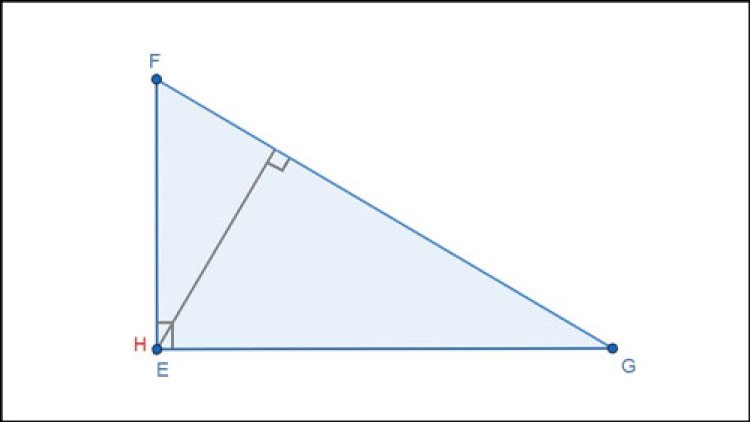
Trực tâm của tam giác tù

Kẻ hai đường cao từ hai đỉnh của tam giác về hai cạnh đối diện, sau đó vẽ thêm một đường cao từ điểm đỉnh góc tù xuống cạnh đối diện. Đường cao này cắt đường cao khác tại một điểm, đó chính là trực tâm của tam giác tù.

Trực tâm của tam giác tù nằm ở miền ngoài tam giác đó.

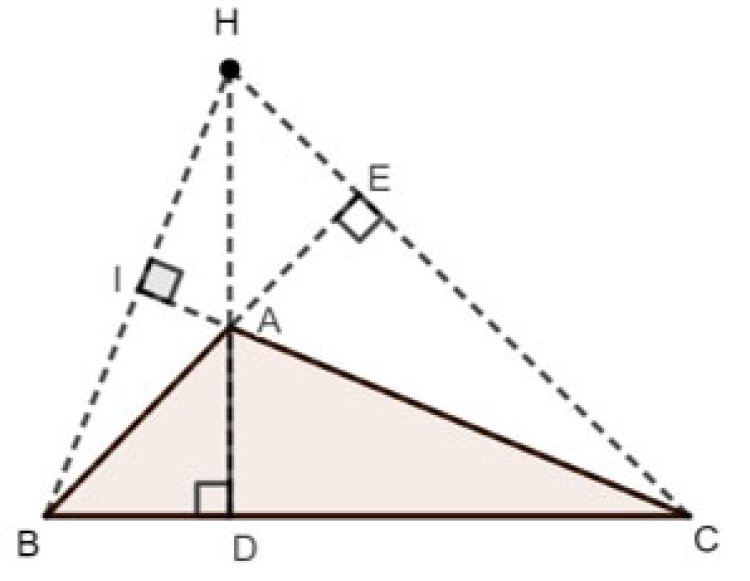
Ví dụ: Tam giác tù BCD có trực tâm H nằm ở miền ngoài tam giác.

Một số bài tập về trực tâm trong tam giác

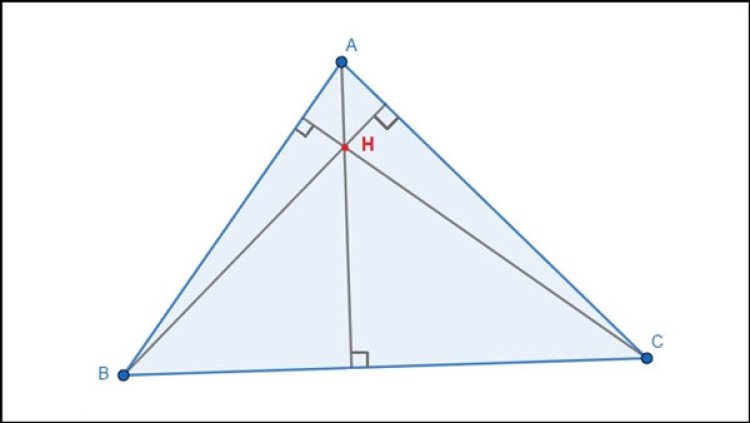
Bài 1: Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC.

Lời Giải:

Trong ΔABC ta có H là trực tâm nên:

AH ⊥ BC, BH ⊥ AC, CH ⊥ AB

Trong ΔAHB, ta có:

AC ⊥ BH

BC ⊥ AH

Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.

Trong ΔHAC, ta có:

AB ⊥ CH

CB ⊥ AH

Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.

Trong ΔHBC, ta có:

BA ⊥ HC

CA ⊥ BH

Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.

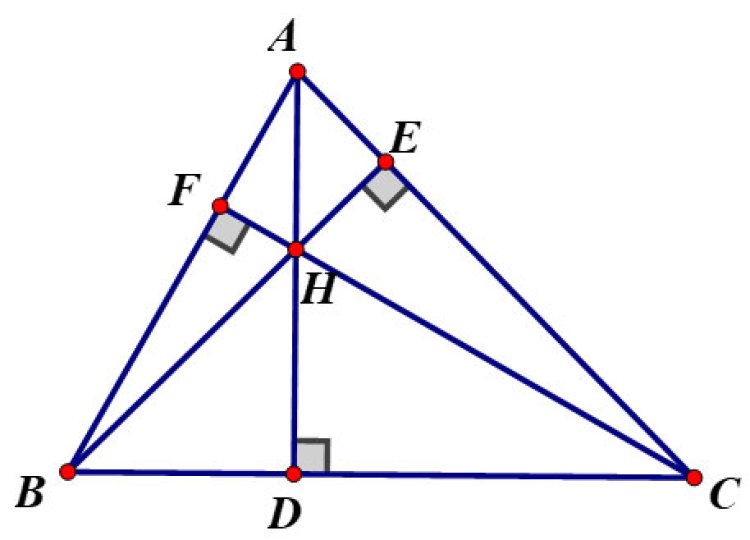
Bài tập 2: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.

Lời Giải:

Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.

⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.

ΔHBC có :

AD ⊥ BC nên AD là đường cao từ H đến BC.

BA ⊥ HC tại F nên BA là đường cao từ B đến HC

CA ⊥ BH tại E nên CA là đường cao từ C đến HB.

AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.

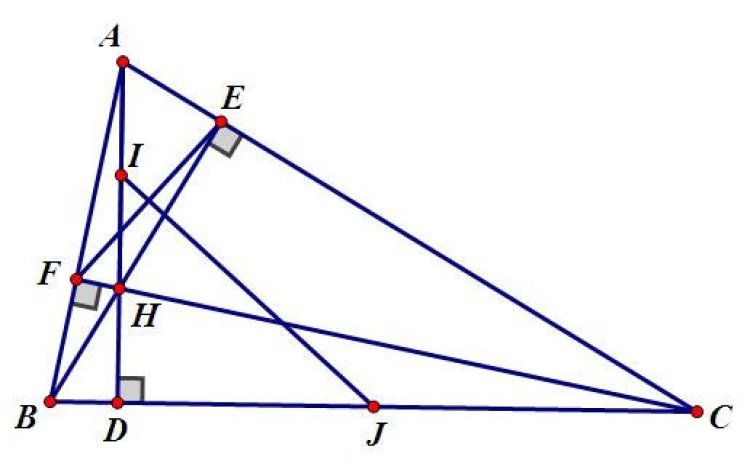
Bài tập 3: Cho △ABC có các đường cao AD; BE; CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.

• a) Chứng minh: JT⊥EFJT⊥EF
• b) Chứng minh: DA là tia phân giác của góc EDF.
• c) Gọi P; Q là hai điểm đối xứng của D qua AB và AC. Chứng minh: P; F; E; Q thẳng hàng.

Lời giải

a) Sử dụng tính chất đường trung bình trong tam giác vuông ta có:

FI = 12AH = EIFJ = 12BC = EJFI = 12AH = EIFJ = 12BC = EJ

Vậy IJ là đường trung trực của EF

b) Tứ giác BFHD và ABDE nội tiếp (đpcm)

c) H là giao điểm 3 phân giác của tam giác EFD

Góc PFB = BFD

Góc DFH = EFH

4 góc này cộng lại = 2.90 =180 => P,E,F thẳng hàng

Tương tự ta có F, E, Q thẳng hàng.

Lời kết

Trong toán học, trực tâm là một điểm quan trọng trong tam giác, đặc biệt được chú ý vì nó mang đến nhiều tính chất và ứng dụng trong hình học. Qua việc tìm hiểu về trực tâm, chúng ta đã đào sâu vào những tính chất cơ bản của nó, từ việc nằm trên đường trung trực đến vai trò quan trọng như tâm của đường tròn ngoại tiếp và trọng tâm của tam giác đều. Việc xác định trực tâm trong tam giác không chỉ là việc xác định một điểm, mà còn là việc hiểu và áp dụng các tính chất hình học vào việc giải quyết các bài toán phức tạp.

Như vậy, qua bài viết này, chúng ta đã có cái nhìn tổng quan về trực tâm, tính chất và cách xác định trong tam giác. Hi vọng rằng những kiến thức này sẽ giúp bạn hiểu sâu hơn về hình học và có thêm cơ sở để giải quyết các vấn đề liên quan đến tam giác một cách thành thạo. Đừng ngại để lại ý kiến của bạn ở phần dưới bài viết nhé.