Cách rút gọn phân số và các bài tập vận dụng

Rút gọn phân số là một trong những kiến thức cơ bản được giảng dạy trong chương trình toán học của lớp 4. Mặc dù là một phép toán cơ bản nhưng lại có ứng dụng rất phổ biến và quan trọng trong toán học cũng như trong các môn học khác sau này. Việc hiểu và thành thạo trong việc rút gọn phân số không chỉ giúp chúng ta giải quyết các bài toán một cách nhanh chóng và chính xác, mà còn giúp chúng ta phát triển khả năng tư duy logic và tính toán.

Trong bài viết này, chúng ta sẽ tìm hiểu về cách rút gọn phân số một cách hiệu quả và nhanh chóng, cùng với đó là những bài tập vận dụng thực tế để củng cố kiến thức. Hãy cùng khám phá và làm quen với một phần quan trọng của toán học hàng ngày!

Rút gọn phân số là gì?

Phân số tối giản

Trước khi bước vào tìm hiểu về rút gọn phân số, các em cần nắm được khái niệm phân số tối giản.

Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào khác 1 (hoặc -1 nếu là số âm).

Ví dụ về phân số tối giản: 5/8 , 15/14, 9/10...

Rút gọn phân số

Rút gọn phân số (hay tối giản phân số) là đưa phân số đó về phân số tối giản. Tức là phân số thu được có tử và mẫu số không thể cùng chia hết cho số nào ngoài trừ 1 (hoặc -1 nếu là các số âm). Nói dễ hiểu, phân số cuối cùng thu được thì mẫu số và tử số có ước chung lớn nhất là 1.

Ví dụ: Rút gọn phân số 12/16 = 12:4/16/4 = 3/4;

Một số chú ý khi rút gọn phân số:

• Không thể rút gọn được phân số tối giản
• Khi rút gọn phân số thì hãy rút gọn thành phân số tối giản
• Hãy xác định ước chung lớn nhất của tử số và mẫu số để rút gọn phân số một cách nhanh chóng.

Hướng dẫn cách rút gọn phân số

Rút gọn phân số là quá trình đơn giản hóa phân số bằng cách chia cả tử số và mẫu số cho ước chung lớn nhất của chúng. Dưới đây là các bước cơ bản để rút gọn phân số:

• Bước 1: Xác định ước số chung lớn nhất (ƯCLN) của tử số và mẫu số: Đầu tiên, ta cần xác định các ước số chung của tử số và mẫu số, sau đó chọn ra ước số lớn nhất trong số đó.
• Bước 2: Chia tử số và mẫu số cho ƯCLN: Sau khi đã xác định được ƯCLN, ta thực hiện phép chia tử số và mẫu số cho ƯCLN này.
• Bước 3: Viết phân số đã rút gọn: Khi đã chia tử số và mẫu số cho ƯCLN, ta viết phân số mới này với tử số và mẫu số đã được rút gọn.

Ví dụ, để rút gọn phân số 12/18 $\frac{\mathrm{<br>}}{}$

• Tìm ƯCLN của 12 và 18. Các ước số của 12 là 1, 2, 3, 4, 6, 12; và các ước số của 18 là 1, 2, 3, 6, 9, 18. ƯCLN của 12 và 18 là 6.

• Chia cả tử số và mẫu số cho 6: 12/6 $\mathrm{<br>}$​=2 và 18/$\frac{\mathrm{<span\; style="font-family:\; \text{'}Source\; Sans\; Pro\text{'},\; sans-serif;\; font-size:\; 14px;">6</span>}}{}<br>$​=3.

• Vậy, phân số đã được rút gọn là 2/3

Như vậy, sau khi thực hiện các bước trên, ta đã rút gọn phân số 12/18 thành 2/3

Ví dụ: Rút gọn phân số 18/72

Lời giải:

Ta thấy 18 và 72 đều chia hết cho 2 nên chia cả tử và mẫu cho 2 ta được:

18/72 = (18 : 2)/(72 : 2) = 9/36

Tiếp tục, cả tử và mẫu đều chia hết cho 9:

9/36 = (9 : 9)/(36 : 9) = 1/4

Vì 14 là phân số tối giản nên ta đã hoàn thành xon phép rút gọn phân số: 18/72 = 1/4

Lưu ý: Khi tử số chia hết cho mẫu số thì phân số có thể rút gọn về số tự nhiên.

Ví dụ: Rút gọn phân số 18/9 = 2

Bài tập rút gọn phân số

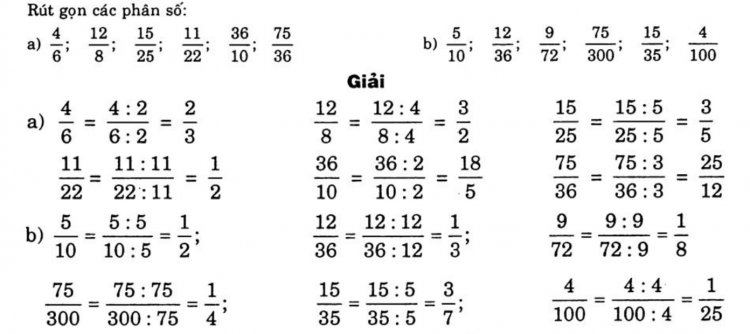
Bài tập 1: Rút gọn các phân số ;

Bài tập 2: Tìm phân số tối giản và phân số chưa tối giản

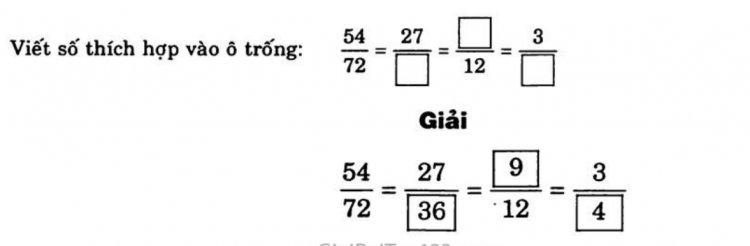
Bài tập 3: Điền số thích hợp vào ô trống

Lời kết

Trên đây là cách rút gọn phân số một cách nhanh chóng và chính xác nhất. Mong rằng với những bài tập vận dụng đã được trình bày, các em sẽ hiểu rõ hơn về cách rút gọn một phân số chưa tối giản và từ đó có thể nắm vững kiến thức này. Việc thực hành và áp dụng trong các bài toán sẽ giúp các em cảm thấy tự tin hơn trong việc giải quyết các vấn đề liên quan đến phân số. Chúc các em thành công và tiếp tục khám phá thêm nhiều kiến thức hay về toán học!