Hình bình hành là gì? dấu hiệu nhận biết và các tính chất của hình bình hành
Nội dung chính [Hiện]
Hình bình hành là một trong những hình học cơ bản và phổ biến trong toán học và hình học. Nó được xác định bởi các đặc điểm đặc trưng và tính chất riêng biệt, giúp ta dễ dàng nhận biết. Hãy cùng tìm hiểu về hình bình hành, từ đặc điểm nhận biết cho đến các tính chất đặc trưng của nó cùng chúng tôi trong bài viết dưới đây.

Hình hình hành là gì?
Hình bình hành là một loại hình học có bốn cạnh và các cạnh đối diện song song và bằng nhau. Nó cũng có bốn góc và hai đường chéo có cùng độ dài và chia nhau ở góc. Đặc điểm này tạo ra các tính chất đặc trưng và dễ nhận biết của hình bình hành.
Một cách khác để mô tả hình bình hành là hình mà có hai cặp cạnh đối diện bằng nhau và song song. Điều này có nghĩa là các cặp cạnh kề nhau có độ dài bằng nhau và các góc giữa chúng cũng bằng nhau.
Hình bình hành thường xuất hiện trong nhiều bối cảnh khác nhau trong toán học và thực tế, và được sử dụng rộng rãi trong các lĩnh vực như hình học, hình học vector, và cả trong tổ hợp và giải tích.
Chúng ta có thể quan sát hình dưới đây để hiểu rõ hơn về hình bình hành
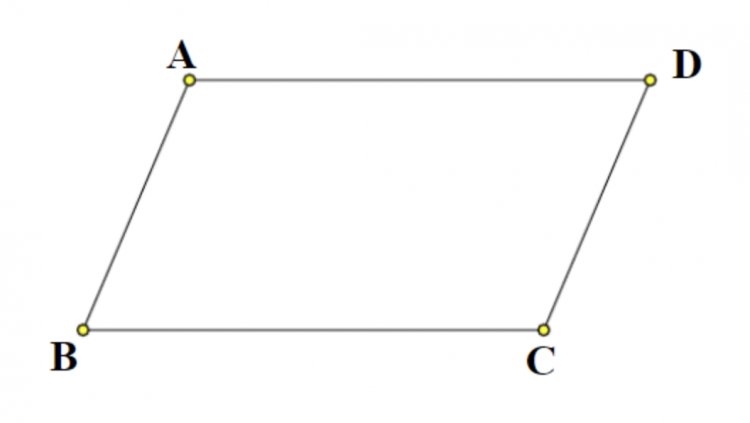
Nhìn vào hình trên chúng ta thấy hình ABCD có các cặp cạnh đối diện AD // BC và AB // CD.
Các dấu hiệu nhận biết tứ giác là hình bình hành.
Để chứng minh một tứ giác là hình bình hành chúng ta cần dựa vào các dấu hiệu nhận biết riêng của hình bình hành. Dưới đây là các dấu hiệu để xác định tứ giác là hình bình hành.
-
Tứ giác có các cặp cạnh đối song song là hình bình hành: Đây là một đặc điểm của hình bình hành. Nếu một tứ giác có các cặp cạnh đối song song, thì nó có thể là một hình bình hành.
-
Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành: Đây là một đặc điểm của hình bình hành. Một tứ giác có một cặp cạnh đối song song và bằng nhau có thể là một hình bình hành.
-
Tứ giác có các góc đối bằng nhau là hình bình hành: Đây cũng là một đặc điểm của hình bình hành. Nếu tứ giác có các góc đối bằng nhau, thì nó có thể là một hình bình hành.
-
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành: Đây là một đặc điểm của hình bình hành. Khi hai đường chéo của tứ giác cắt nhau tại trung điểm của mỗi đường, thì tứ giác đó có thể là một hình bình hành.
Tính chất của hình bình hành
Hình bình hành có các tính chất như sau.
-
Các cạnh đối diện song song và bằng nhau: Điều này có nghĩa là hai cặp cạnh đối diện trong hình bình hành có cùng độ dài và song song với nhau.
-
Các góc đối diện bằng nhau: Các góc đối diện trong hình bình hành có cùng độ lớn, tức là các góc tương tự nhau.
-
Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường, tức là chúng chia đôi nhau.
Ví dụ cụ thể về hình bình hành là hình vuông. Hãy xem xét một hình vuông với các đặc điểm sau:
- Các cạnh của hình vuông đều có độ dài bằng nhau và đối diện với nhau.
- Các góc của hình vuông đều có độ lớn bằng 90 độ và đối diện với nhau.
- Hai đường chéo của hình vuông cắt nhau tại trung điểm của mỗi đường.
Công thức tính chu vi hình bình hành
Chu vi của một hình chính là tổng chiều dài các cạnh. Do hình bình hành là một tứ giác đặc biệt với các cặp cạnh đối bằng nhau nên ta có công thức tính chu vi hình bình hành là:
Chu vi của một hình bình hành bằng hai lần tổng một cặp cạnh kề nhau bất kỳ.
Công thức: C = 2 * (a + b)
Trong đó:
- C là chu vi hình bình hành
- a, b là chiều dài hai cạnh của hình bình hành
Ví dụ: Hình bình hành ABCD có 2 cạnh dài lần lượt là 4cm và 6cm. Hãy tính chu vi hình bình hành ABCD.
Lời giải:
Áp dụng công thức tính chu vi hình bình hành:
C = 2 * (a + b) = 2 * (4 + 6) = 20cm
Công thức tính diện tích hình bình hành
Diện tích hình bình hành là toàn phần mặt phẳng ta có thể thấy được của hình bình hành. Công thức tính diện tích hình bình hành như sau:
S = a * h
Trong đó:
S là diện tích
a là cạnh đáy
h là chiều cao
Chiều cao được xác định chính là khoảng cách của cặp cạnh đối. Bạn nối từ đỉnh đến đáy của hình bình hành sẽ được chiều cao của nó.
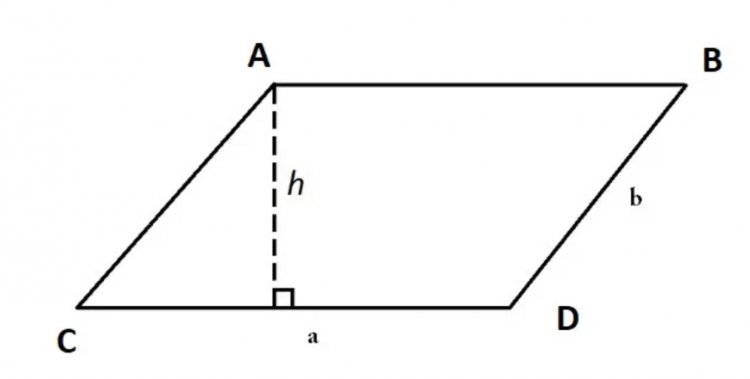
Ví dụ: Hình bình hành ABCD có cạnh đáy dài 8cm, chiều cao 4cm. Hãy tính diện tích của hình bình hành ABCD.
Lời giải:
Áp dụng công thức tính diện tích hình bình hành ta có:
S = a * h = 8 * 4 = 32cm2
Bài tập vận dụng về hình bình hành
Bài 1. Cho hình bình hành ABCD.
a, Gọi E, F theo thứ tự là trung điểm của AB và CD. Chứng minh: AF // CE
b, Gọi M, N theo thứ tự là giao điểm của BD với AF, CE. Chứng minh: DM = MN = NB
Lời giải:
Hình bình hành ABCD và các điểm E, F, M, N được biểu diễn trong hình dưới đây:
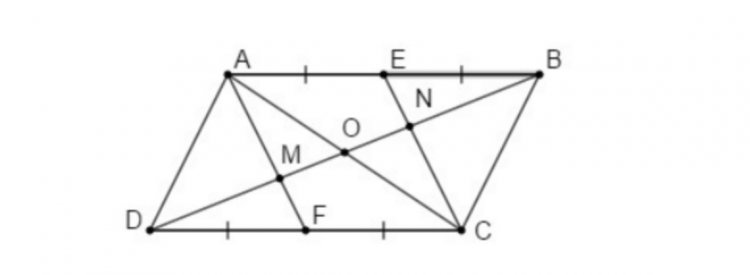
a, Theo tính chất của hình bình hành ta có: AB = CD
mà E thuộc AB và F thuộc DC ⇒ AE // FC
Vì E, F là trung điểm của AB và CD
⇒ AE = EB = DF = FC
Trong tứ giác AECF có:
AE = FC và AE // FC nên AECF là hình bình hành (Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành)
⇒ AF // EC (tính chất của hình bình hành)
b, Gọi AC giao BD tại O
Xét tam giác ADC có:
DO, AF là trung tuyến (AO = OC, DF = FC)
AF giao DO tại M
⇒ M là trọng tâm của tam giác ADC
⇒ DM = 2/3 DO = 2/3 BO (1)
và OM = 1/3 DO = 1/3 BO (2) (do DO = BO)
Xét tam giác ABC có:
BO, CE là trung tuyến
BO giao CE tại N
⇒ N là trọng tâm của tam giác ABC
⇒ BN = 2/3 BO (3)
và ON = 1/3 BO (4)
Từ (2), (4) ⇒ MN = OM + ON = 1/3 BO + 1/3 BO = 2/3 BO (5)
Từ (1), (3) và (5) ⇒ DM = BN = MN
Bài 2. Chọn cụm từ thích hợp điền vào chỗ trống: “Tứ giác có hai đường chéo…thì tứ giác đó là hình bình hành”
A. Bằng nhau
B. Cắt nhau
C. Cắt nhau tại trung điểm mỗi đường
D. Song song
Đáp án C
Bài 3. Hãy chọn câu đúng: Cho hình bình hành ABCD, E là trung điểm của AB, F là trung điểm của CD. Khi đó:
A. DE = BF
B. AE // BF
C. CE = BF
D. DE = EB
Đáp án A
Bài 4. Hình bình hành ABCD có góc A lớn gấp 3 lần góc B. Số đo các góc của hình bình hành là:
A. Góc A = góc D = 120°, góc B = góc C = 60°
B. Góc A = góc C = 100°; góc B= góc D = 50°
C. Góc A = góc C = 60°, góc B = góc D = 120°
D. Góc A = góc C = 135°, góc B = góc D = 45°
Đáp án D
Lời giải: Gọi số đo góc B là x ⇒ số đo góc A là 3x
Do A và B là 2 góc kề nhau nên tổng số đo 2 góc là 180 độ
3x + x = 180 ⇒ 4x = 180 ⇒ x = 45 độ.
Vậy góc A = góc C = 135 độ, góc B = góc D = 45 độ
Bài 5. Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo, E và F theo thứ tự là trung điểm của OD và OB.
a, Chứng minh: AE // CF
b, Gọi AE giao CD tại K. Chứng minh: DK = 1/2 KC
Lời giải:
Theo bài ra ta có hình sau:
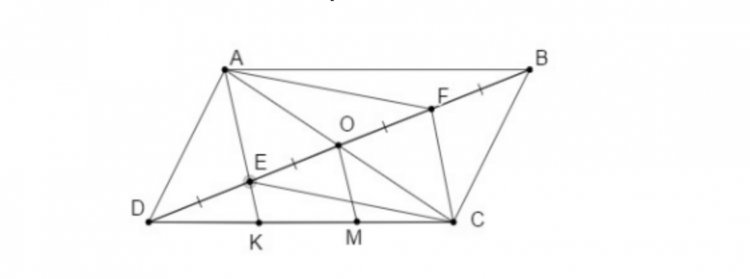
a, AC giao BD tại O ⇒ OD = BO
Vì E, F là trung điểm của DO và BO ⇒ DE = EO = OF = FB
Xét tứ giác AFCE có:
AC giao EF tại O nên:
OA = OC, OE = OF
⇒ AFCE là hình bình hành (theo dấu hiệu nhận biết)
⇒ AE // CF (tính chất của hình bình hành)
b, Từ O kẻ OM // EK
Xét tam giác DOM có:
OM // EK
và E là trung điểm của DO
⇒ K là tung điểm của DM ⇒ DK = KM (1)
Xét tam giác CDK có:
OM // AK
và O là trung điểm của AC
⇒ M là trung điểm của KC ⇒ CM = KM (2)
Từ (1) và (2) ⇒ DK = KM = CM
mà KM + CM = KC
⇒ DK = 1/2 KC
Bài 6. Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD.
a, Chứng minh: EFGH là hình bình hành
b, Cho AD = a, BC = b. Tính chu vi hình bình hành EFGH
Lời giải:
Theo bài ra ta có hình vẽ sau:
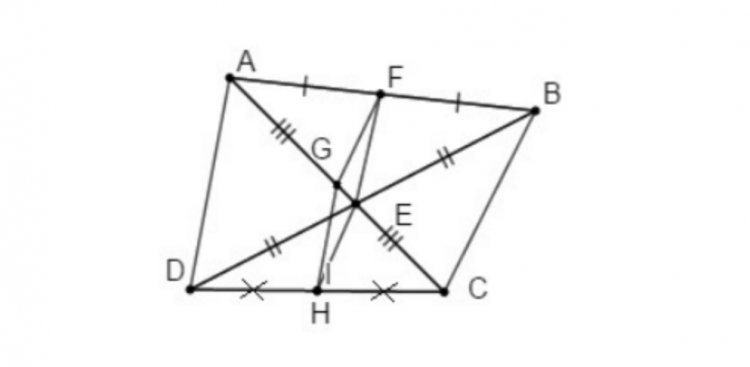
a, Xét tam giác ABD có:
F và E lần lượt là trung điểm của AB, BD ⇒ EF là đường trung bình của tam giác ABD
⇒ EF // AD (1)
và EF = 1/2 AD (2)
Tương tự, ta có GH là đường trung bình của tam giác ACD
⇒ GH // AD (3)
và GH = 1/2 AD (4)
Từ (1) và (3) ⇒ EF // GH
(2) và (4) ⇒ EF = GH
⇒ tứ giác GHEF là hình bình hành
b, Ta có: GH = EF = 1/2 AD = 1/2 a
FG = HE = 1/2 BC = 1/2 b
Chu vi hình bình hành GFEH là: C = (1/2 a + 1/2 b).2 = a + b
Bài 7. Cho hình bình hành ABCD. Lấy N thuộc AB, M thuộc CD sao cho AN = CM. Chứng minh:
a, AM // CN
b, DN = BM
c, AC, BD, MN đồng quy
Lời giải:
Từ bài ra ta có hình vẽ sau:
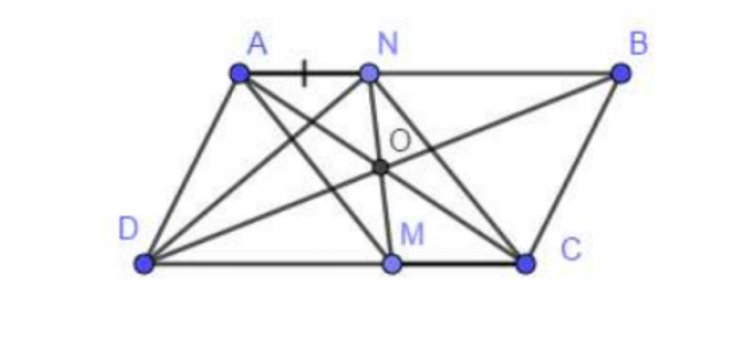
a, Xét tứ giác ABCD có:
AN = CM
AN // CM (do AB//CD)
⇒ ANCM là hình bình hành
⇒ AM // CN
b, Ta có: BN = AB – AN
DM = DC – CM
mà AB = DC, AN = CM
⇒ BN = DM
mà BN // DM (do AB // CD)
⇒ BNDM là hình bình hành (theo dấu hiệu nhận biết)
⇒ DN = BM (tính chất)
c, Gọi AC giao BD tại O (1)
⇒ O là trung điểm của AC và BD
Ta có: ANCM là hình bình hành và O là trung điểm của đường chéo AC
⇒ O là trung điểm của MN
⇒ O thuộc MN (2)
Từ (1) và (2) ⇒ AC, BD, MN đồng quy
Trên đây là những thông tin về hình bình hành và các bài tập vận dụng. Mong rằng qua bài viết này sẽ giúp bạn có thêm được nhiều kiến thức hữu ích. Chúc bạn thành công trong việc áp dụng những kiến thức này vào thực tế và phát triển khả năng tư duy hình học của mình. Đừng ngần ngại thảo luận về hình bình hành bên dưới bài viết này.






